Видео

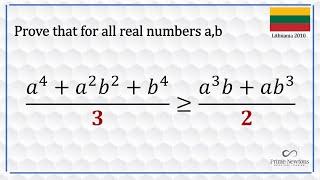
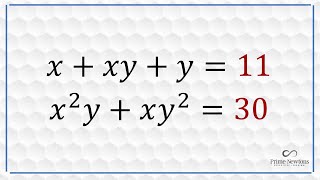
there seems to be some issue in the logic of the solution

Isnt u going to +- infinity as t approaches 0?

You are just incredible

That's the amazing topic sir I'm not actually see even in my uni lifee thanks n love from pakistan🇵🇰

Appreciate your enthusiasm ❤

Do you guys know there is something called pentation? I was searching this up and found out pentation is even larger... Brain dead

Bros cooking

really enjoyable

Note that: • the equation are cyclical • as RHS of any one equation is integer x, y and z are integers. The reasons are as follows: * if any one of x, y, and z not an integer then all equation's RHS will not be integer * if any two of x, y, and z not an integer RHS of one equation will be an integers, but those of the other ones will not. * if x, y, z are all not integer, RHS of all equations will not be integer. (x+y+z)²=x²+y²+z²+2(xy+yz+zx) 9=3+2(xy+yz+zx) xy+yz+zx=3 (x+y+z)³=x³+y³+z³ +3(x+y+z)(xy+yz+zx)-3xyz 3³=3+3³-3xyz --> xyz=1 xyz=1 implies that • x=y=z=1 • any one of x, y, and z is 1 and the other two -1 Hence (x,y,z)={(1,1,1),(1,-1,-1),(-1,1,-1), (-1,-1,1)} A simpler way to solve is to use Newton-Girard method

How i ms this man so clever

what app are you using?

🎉🎉🎉🎉

🎉🎉🎉🎉

what a nice video to watch

x+y+z=3 x^2+y^2+z^2+2xy+2xz+2yz=9 xy+xz+yz=(9-3)/2=3 x(y+z)+yz=3 x(3-x)+yz=3 x^2-3x+3=yz (x^2+y^2+z^2)(x+y+z)=9 x^3+y^3+z^3+xy(x+y)+xz(x+z)+yz(y+z)=9 xy(3-z)+xz(3-y)+yz(3-x)=6 3(xy+xz+yz)-3xyz=6 xyz=1 yz=1/x x(y+z)+yz=3 x(3-x)+1/x=3 x^3-3x^2+3x-1=0 (x-1)^3=0 x=1 xz=1/y y(x+z)+1/y=3 y=1 xy=1/z z(x+y)+1/z=3 z=1 <x,y,z>=<1,1,1>

Nice problem and video! A couple of minor issues with the proof given: 1) At 5:47 it is concluded that for positive a,b: (a^2+b^2)/2 >= ab In fact this is true for all reals a,b and indeed this is assumed and needed later at 10:27. To prove this inequality for all reals a,b: (a-b)^2 ≥ 0 <=> a^2 - 2ab + b^2 ≥ 0 <=> (a^2 + b^2)/2 ≥ ab 2) At 6:16 you square the above inequality. This step is guaranteed to be true only if the LHS and RHS are positive. However ab is not always positive and in general it is not valid to say that p>q implies p^2>q^2. For example: 1>-10 is true but 1^2>(-10)^2 is false. As it happens, in this case we are okay because the LHS and RHS are not independent values: [(a^2 + b^2)/2]^2 ≥ (ab)^2 <=> (a^4 + 2(ab)^2 + b^4) ≥ 4(ab)^2 <=> a^4 - 2(ab)^2 + b^4 ≥ 0 <=> (a^2 - b^2)^2 ≥ 0 This last line is clearly true meaning that the squared inequality holds. An alternative proof of the original inequality: 2(a^4 + (ab)^2 + b^4) ≥ 3(ba^3 + ab^3) <=> 2[(a^2 + b^2)^2 - (ab)^2] ≥ 3ab(a^2 + b^2) <=> 2[((a+b)^2 - 2ab)^2 - (ab)^2] ≥ 3ab((a+b)^2 - 2ab) <=> 2((a+b)^2 - 2ab)^2 - 2(ab)^2 ≥ 3ab(a+b)^2 - 6(ab)^2 <=> 2((a+b)^4 - 4ab(a+b)^2 + 4(ab)^2) - 2(ab)^2 ≥ 3ab(a+b)^2 - 6(ab)^2 <=> 2(a+b)^4 - 11ab(a+b)^2 + 12(ab)^2 ≥ 0 <=> (2(a+b)^2 - 3ab).((a+b)^2 - 4ab) ≥ 0 [*] (a+b)^2 - 4ab = a^2 + 2ab + b^2 - 4ab = a^2 - 2ab + b^2 = (a-b)^2 ≥ 0 2(a+b)^2 - 3ab = 2(a^2 + 2ab + b^2) - 3ab = 2(a^2 + b^2) + ab Let a=r.cos(t) and b=r.sin(t): = 2r^2(cos^2(t) + sin^2(t)) + r^2.sin(t).cos(t) = r^2(2 + sin(2t)/2) ≥ r^2(2 - 1/2) = (3/2)r^2 ≥ 0 So the 2 terms on the LHS of [*] are indeed non-negative.

I am an Indian and i am really obsessed by your teaching ....... you have that art to teach and make things clear to us . i show my gratitude respectively.❤❤❤🎉🎉😊😊😊😊 you have 1 more subscriber 🎉🎉🎉🎉

maybe 16:37 should not be "or" but be "and" consider the meaning of vieta's formula

Thanks for this amazing video 😊

Mate i'm studying for a test, yet your attitude is so fun, i'm actually starting to like linear algebra lol. Thank you man.

respect a remake keep growing your channel

Thanks for your interesting problem. Here is the way I solved it. Of course, I didn't look at your solution. Tell me, if you like mine. Greetings and keep up the good work, with sharing us challenging problems. RECALL Solve the problem with all solutions reals and complex. (i) x+y+z=3 (ii) x^2+y^2+z^2=3 (iii) x^3+y^3+z^3=3 Let's square equation (i) x+y+z=3, then (i)^2 (x+y+z)^2=3^2 x^2+y^2+z^2+2(xy+yz+zx)=3^2 and from (ii), we have 3+2(xy+yz+zx)=3^2 then (xy+yz+zx)=(3^2-3)/2=3 so (xy+yz+zx)=3 Let equation (xy+yz+zx)=3 be (iv) Let's cube equation (i) x+y+z=3, then (i)^3 (x+y+z)^3=3^3 x^3+y^3+z^3+3xy(x+y)+3yz(y+z)+3zx(z+x)+6xyz=3^3 and from (iii), we have 3+3xy(x+y)+3yz(y+z)+3zx(z+x)+6xyz=3^3 moreover from (i), we have y+z=3-x and z+x=3-y and x+y=3-z so injecting those three equalities in the above one we have 3+3xy(3-z)+3yz(3-x)+3zx(3-y)+6xyz=3^3 then 3+3^2.(xy+yz+zx)-3xyz-3xyz-3xyz+6xyz=3^3 3+3^2.(xy+yz+zx)-3xyz=3^3 and from (iv) we have 3+3^2.3-3xyz=3^3 so we have 3-3xyz=0 then xyz=1 Let equation xyz=1 be (v) From following equations (i) x+y+z=3 (iv) xy+yz+zx=3 (v) xyz=1 we recognise the symetric functions of the roots (x;y;z) of a third degree equation at^3+bt^2+ct+d=0 with the following relations between the coefficients and the roots as below (those relations being called as well as the Vieta's formulas) x+y+z=-b/a xy+yz+zx=c/a xyz=-d/a so that -b/a=3 c/a=3 -d/a=1 If we choose a=1, we have b=-3, c=3 and d=1, leading to following equation t^3-3t^2+3t-1=0 that can be written as follows (t-1)^3=0 which gives t-1=0 and finally t=1 showing that the equation has got a triple root of value 1. To conclude the system has got the only solution (x;y;z)=(1;1;1) END

7:27 gives me chill 😂

Notice that since S_1, S_2, and S_3 are functions of x + y + z, x^2 + y^2 + z^2, and x^3 + y^3 + z^3, if you have any one solution (x_0,y_0,z_0) to a system x + y + z = a, x^2 + y^2 + z^2 = b, x^3 + y^3 + z^3 = c, all of the solutions will be the permutations of (x_0,y_0,z_0) since doing what was done here will lead to (t - x_0)(t - y_0)(t - z_0) = 0 in the end.

Accelerated Girard-Newton method: t^3 -(x+y+z)t^2 +(xy+xz+yz)t -xyz=0 t^3-3t^2+3t-xyz=0 Let's replace t with x,y,z : x^3-3x^2+3x-xyz=0 (1) y^3-3y^2+3y-xyz=0 (2) z^3-3z^2+3z -xyz=0 (3) (1)+(2)+(3) x^3+y^3+z^3-3(x^2+y^2+z^2)+3(x+y+z)-3xyz=0, 3-3*3+3*3-3xyz=0, 3=3xyz xyz = 1. Historically, Girard was the first to discover the connection between symmetric polynomials and the sum of powers solutions of a polynomial equation. It doesn't always have to be Newton Prime. At least once to be Second. Never stop learning.😎

Iam 16 and i try to solve it and finally i do it😆

The optimal triangle is the isoceles triangle (a=b=c) : one can prove geometrically( by the so-called Steiner symmetrization ) that for given circumference the isoceles triangle has the largest area .This is closely related isoperymetric inequality which states for a lane domain of given circumference the circle has the largest area. If a+b+c is minimal for given area then a^2+b^2+c^2 is also minimal. This problem has interesting connections to other geometric questions.

Input (1 | -1 2 | 4)^100 = (-515377520732011328501159929309162469708701111249 | -515377520732011329768810529537391871205404316625 1030755041464022659537621059074783742410808633250 | 1030755041464022660805271659303013143907511838626) Result True

Terimakasih🙏 Sangat jelas, walaupun saya tidak terlalu paham bahasa Inggris. Tulisan Anda sangat sangat rapi.

Man love watching your video , it's fabulous

We already heard about "Mersenne Primes".

Sytstem of equations with symmetric polynomials In fact there are special case of symmetric polynomials called power sums There are Newton-Girard formulas which allow to express power sums in terms of elementary symmetric polynomials Elementary symmetric polynomials appear in Vieta formulas To use Vieta formulas we must have elementary symmetric polynomials

I was thinking that with the cubic there can only be three solutions. (1,1,1) is a solution, found by observation. But because the equations are symmetric, this must be a triple root. So there are no other solutions.

Very cool. So asking for potential complex roots, they were hoping to mislead you forcing you to investigate further.

Amazing how easy or difficult this channel's problems get. Thanks for the help!

Beautiful explanation, really liked the solving method!

Solved in 0.1 seconds 😂...

You are explained very well! Continue to teaching!

We can manipulate the given inequality into a sort of sum of squares form. First, notice that we only need to prove the inequality for positive a and b, since when a and/or b are negative, the LHS remains the same but the RHS can only decrease or remain the same. Now, for simplicity, we can get rid of the denominators by multiplying the inequality by 6 and move all terms to LHS yielding: 2a^4 + 2b^4 + 2a^2 b^2 - 3a^3 b - 3a b^3 >= 0 This, in turn, can be represented as a (sort of) sum of squares and fourth powers as: (a - b)^4 + (a^2 - b^2)^2 + ab (a-b)^2 >= 0 The "sort of" is due to the fact that there is ab in front of the last square, but since we already justified focusing on non-negative values of a and b in the proof, we are good to go.

³2 is 16 because of 2²² which means 2²×²=2⁴ therefore making 2×2×2×2=16, that is very confusing